Derajat kebebasan adalah suatu parameter fisika yang independen, biasa disebut dimensi, dalam deskripsi formal merupakan keadaan suatu sistem fisika. Himpunan semua dimensi dari suatu sistem dikenal sebagai ruang fasa.
Definisi
Dalam fisika, derajat kebebasan suatu sistem merupakan deskripsi formal dari parameter yang berkontribusi untuk keadaan dari sistem fisika. Juga bisa didefinisikan sebagai suatu angka minimum yang diperlukan untuk menentukan koordinat posisi suatu partikel atau sistem partikel. Dalam mekanika, partikel titik dapat bergerak secara bebas tiga arah dalam ruang. Dengan demikian, momentum suatu partikel terdiri atas tiga komponen, masing-masing disebut derajat kebebasan. Suatu sistem terdiri atas N partikel bebas sehingga memiliki total derajat kebebasan 3N. Demikian juga dalam mekanika statistik, derajat kebebasan adalah angka skalar tunggal yang menggambarkan keadaan mikro suatu sistem. Spesifikasi semua keadaan mikro sistem adalah suatu titik dalam ruang fasa sistem. Derajat kebebasan yang digunakan tidak bergantung pada variabel lain. Sebagai contoh, dalam model rantai ideal 3D, dua sudut yang diperlukan untuk menjelaskan masing-masing orientasi monomer.Contoh: Gas diatomik
- 3N = 6 = 3 + 1 + 2.
- 3 N = 3 + 3 + (3 N - 6)
Selain itu, menghitung derajat kebebasan dapat juga menggunakan nilai minimum koordinat yang diperlukan untuk menentukan posisi. Hal ini dilakukan sebagai berikut: 1. Untuk partikel tunggal diperlukan 2 koordinat pada bidang 2-D untuk menentukan posisinya dan derajat kaebebasan pada bidang 3-D adalah 3. 2. Untuk sistem yang terdiri atas 2 partikel (molekul diatomik) pada bidang 3-D dengan jarak konstan (d) memiliki derajat kebebasan 5. Satu partikel memiliki koordinat (x1,y1,z1) dan koordinat lainnya (x2) dan (y2). Persamaan untuk jarak antara 2 koordinat atom (
 ) diperoleh nilai yang mengandung (z2). (Catatan:x1, x2, y1, y2, z1, atau z2 bisa aja tidak diketahui.) Berlawanan dengan teorema equipartisi klasik, pada gerak vibrasi molekul biasanya kapasitas suhu
dapat diabaikan. Hal ini menyebabkan derajat kebebasan dibekukan karena
jarak antara energi nilai eigen melebihi energi yang sesuai dengan suhu
lingkungan (kT). Dalam tabel berikut derajat kebebasan diabaikan karena
efeknya yang kecil terhadap energi total. Namun, pada suhu yang sangat
tinggi derajat kebebasan tidak bisa diabaikan.
) diperoleh nilai yang mengandung (z2). (Catatan:x1, x2, y1, y2, z1, atau z2 bisa aja tidak diketahui.) Berlawanan dengan teorema equipartisi klasik, pada gerak vibrasi molekul biasanya kapasitas suhu
dapat diabaikan. Hal ini menyebabkan derajat kebebasan dibekukan karena
jarak antara energi nilai eigen melebihi energi yang sesuai dengan suhu
lingkungan (kT). Dalam tabel berikut derajat kebebasan diabaikan karena
efeknya yang kecil terhadap energi total. Namun, pada suhu yang sangat
tinggi derajat kebebasan tidak bisa diabaikan.| Monatomik | Molekul linear | Non-Linear molekul | |
|---|---|---|---|
| Posisi (x, y and z) | 3 | 3 | 3 |
| Rotasi (x, y and z) | 0 | 2 | 3 |
| Vibrasi | 0 | 3N - 5 | 3N - 6 |
| Total | 3 | 3N | 3N |
Derajat kebebasan Independen
Derajat kebebasan terdiri atas suatu sistem yang independen jika energi assosiatif diatur bisa ditulis sebagai berikut:
suatu sistem yang independen jika energi assosiatif diatur bisa ditulis sebagai berikut:  di mana
di mana 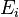 adalah fungsi dengan variabel tunggal
adalah fungsi dengan variabel tunggal  . example: jika
. example: jika 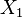 and
and  memiliki 2 derajat kebebasan, dan
memiliki 2 derajat kebebasan, dan  adalah energi assosiatif:
adalah energi assosiatif:-
- Jika
 , dengan dua derajat kebebasan yang independen.
, dengan dua derajat kebebasan yang independen. - Jika
 , dengan dua derajat kebebasan yang tidak independen. Istilah yang melibatkan produk
, dengan dua derajat kebebasan yang tidak independen. Istilah yang melibatkan produk 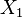 dan
dan  adalah istilah kopling, yang menggambarkan interaksi antara dua derajat kebebasan.
adalah istilah kopling, yang menggambarkan interaksi antara dua derajat kebebasan.
- Jika
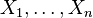 semua statistik independen satu sama lain.
semua statistik independen satu sama lain.Untuk i dari 1 to N, dengan iderajat kebebasan
 didistribusikan berdasarkan distribusi Boltzmann. Probability fungsi kerapatan mengikuti:
didistribusikan berdasarkan distribusi Boltzmann. Probability fungsi kerapatan mengikuti: ,
,
 menunjukkan mean rata-rata jumlah.
menunjukkan mean rata-rata jumlah.Energi internal sistem merupakan jumlah dari rata-rata energi asosiatif untuk setiap derjat kebebasan:
Demonstrasi
Sebuah pertukaran energi sistem dalam bentuk panas dengan lingkungannya dan jumlah partikel dalam sistem tetap. Hal ini terkait dengan sistem dalam ansambel kanonik. Perhatikan bahwa dalam mekanika statistik, hasil yang ditunjukkan untuk sistem dalam ansambel tertentu tetap untuk sistem ini pada batas termodinamika dalam ansambel apapun. Dalam ansambel kanonik, kesetimbangan termodinamika, keadaan dari sistem didistribusikan di antara semua keadaan mikro berdasarkan distribusi Boltzmann. Jika suhu sistem dan
suhu sistem dan  konstanta Boltzmann, maka probabilitas fungsi kerapatan yang terkait untuk setiap keadaan mikro adalah sebagai berikut:
konstanta Boltzmann, maka probabilitas fungsi kerapatan yang terkait untuk setiap keadaan mikro adalah sebagai berikut: ,
,
![\ ldots X_N </ math> adalah [[statistik independen ]] satu sama lain.
Setiap fungsi <math>p_i](http://upload.wikimedia.org/math/2/3/b/23b827de812631a56285d2d0cae18553.png) adalah Konstanta Normalisasi, mengikuti bahwa
adalah Konstanta Normalisasi, mengikuti bahwa  adalah probabiliti fungsi kerapatan dari derajat kebebasan
adalah probabiliti fungsi kerapatan dari derajat kebebasan  , untuk i dari 1 sampai N.
, untuk i dari 1 sampai N.Sehingga energi internal dari sistem merupakan energi rata-rata. Energi dari derajat kebebasan
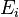 adalah fungsi dari variabel tunggal
adalah fungsi dari variabel tunggal  . Jika
. Jika  adalah statistik independent satu sama lain, maka energi
adalah statistik independent satu sama lain, maka energi  juga statistik independen satu sama lain. Total energi internal dari sistem bisa ditulis:
juga statistik independen satu sama lain. Total energi internal dari sistem bisa ditulis:Derajat Kebebasan Kuadratik
Suatu derajat kebebasan adalah kuadratik apabila the energi terkait dengan derajat kebebasan, dapat ditulis sebagai
adalah kuadratik apabila the energi terkait dengan derajat kebebasan, dapat ditulis sebagai ,
,
 adalah kombinasi linear dari setiap derajat kebebasan kuadratik.
adalah kombinasi linear dari setiap derajat kebebasan kuadratik.contoh: jika
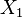 dan
dan  adalah dua derajat kebebasan, dan
adalah dua derajat kebebasan, dan  adalah energi asosiatif:
adalah energi asosiatif:-
- Jika
 , dengan dua derajat kebebasan yang tidak independen dan non-kuadratik.
, dengan dua derajat kebebasan yang tidak independen dan non-kuadratik. - Jika
 , dengan dua derajat kebebasan yang independen and non-quadratik.
, dengan dua derajat kebebasan yang independen and non-quadratik. - Jika
 , dengan dua derajat kebebasan yang tidak independen dan kuadratik.
, dengan dua derajat kebebasan yang tidak independen dan kuadratik. - Jika
 , dengan dua derajat kebebasan yang independen dan kuadratik.
, dengan dua derajat kebebasan yang independen dan kuadratik.
- Jika
Derajat Kebebasan Independen dan Kuadratik
 adalah derajat kebebasan kuadratik dan independen apabila energi
assosiatif untuk keadaan mikro suatu sistem bisa dipresentasikan sebagai
berikut:
adalah derajat kebebasan kuadratik dan independen apabila energi
assosiatif untuk keadaan mikro suatu sistem bisa dipresentasikan sebagai
berikut:Teorema Equipartisi
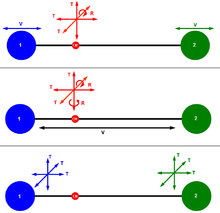
Pada batasan klasik mekanika statisti, pada equilibrium termodinamika, energi internal dari suatu sistem N derajat kebebasan independen dan kuadratik adalah:http://id.wikipedia.org
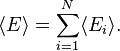






Tidak ada komentar:
Posting Komentar